2°A Matemáticas, 1 - 5 de Marzo

  

Materia: M a t e m á t i c a s    I I

Nombre del docente: Lizbeth Hamid Carpinteyro Montiel

Correo electrónico: halimoca@hotmail.com

Fecha: Del lunes 1 al viernes 5 de marzo del año 2021.

¡Hola jóvenes!

Si tienen dudas comuníquense conmigo mediante el correo electrónico o enviando un mensaje por whatsApp. En caso de que sea por correo electrónico en ASUNTO coloquen DUDAS y serán resueltas a la mayor brevedad posible. 

Recuerden que al enviar sus actividades por correo electrónico deben escribir en ASUNTO: Nombre completo, Grado y Grupo.

 

INDICACIONES GENERALES:

• Copia el tema completo e indicaciones en tu libreta de matemáticas.
• Envía las fotografías al correo electrónico, debes revisar que las fotografías sean claras y se pueda leer perfectamente tu trabajo, de lo contrario se te regresará sin evaluar.
• Colocar nombre completo, grado y grupo a CADA HOJA.

 

CLASE A DISTANCIA:

Entrar a la clase en línea; día LUNES.

1._ Entrar con el nombre completo del alumno.

2._ El enlace de la clase se enviara 5 minutos antes de la clase en el grupo de whatsApp de Matemáticas.

La clase será de 2:25 a 3:05 pm los días LUNES.

ACTIVIDAD 1.

Eje: Número, Álgebra y Variación.

Tema: Funciones.

Aprendizaje Esperado: Analiza y compara situaciones de variación lineal y proporcionalidad inversa a partir de sus representaciones tabular, gráfica y algebraica. Interpreta y resuelve problemas que se modelan con este tipo de variación, incluyendo fenómenos de la física y otros contextos.

Énfasis: Analizar y comparar situaciones de variación lineal y proporcionalidad inversa.

 

Analiza la información de la siguiente situación y anota en tu cuaderno tus dudas y hallazgos.

¿Has escuchado en alguna ocasión que la temperatura en alguna ciudad es de 80 grados Fahrenheit? ¿Esto es posible?

Si es posible, se debe analizar la relación entre los grados Fahrenheit y los grados Celsius, se trata de una relación de variación lineal que está dada por la siguiente fórmula:

 

Donde:

°F: es la temperatura en grados Fahrenheit.

°C: representa la temperatura en grados Celsius.

 

Situación-problema: grados Fahrenheit 

En un día soleado en el puerto de Veracruz, anunciaron que nos encontrábamos a 80 grados Fahrenheit.

1._ ¿Qué significa esto?

2._ ¿Estaba haciendo “mucho calor”?

 

ACTIVIDAD 2.

Eje: Número, Álgebra y Variación.

Tema: Funciones.

Aprendizaje Esperado: Analiza y compara situaciones de variación lineal y proporcionalidad inversa a partir de sus representaciones tabular, gráfica y algebraica. Interpreta y resuelve problemas que se modelan con este tipo de variación, incluyendo fenómenos de la física y otros contextos.

Énfasis: Analizar y comparar situaciones de variación lineal y proporcionalidad inversa.

 

Características de la variación proporcional directa:

* Su gráfica es una línea recta.

* Cuando la variable independiente aumenta, también aumenta la variable dependiente, siempre en la misma proporción.

* Existe una constante (k) de proporcionalidad.

* La recta que la representa pasa por el origen del plano cartesiano.

Para verificar sí la relación entre los grados Fahrenheit y los grados Celsius cumplen con las características mencionadas. Realiza la siguiente tabla.

 

C a r a c t e r í s t i c a s	Si  o  No
Su gráfica es una línea recta.
Cuando la variable “x” aumenta, también aumenta la variable “y”, siempre en la misma proporción.
Existe una constante de proporcionalidad “k”.
La recta que la representa pasa por el origen del plano cartesiano.

 

En la columna de la derecha deberás escribir Sí o No según corresponda. Si cumple con todas esas propiedades, entonces se trata de una relación de proporcionalidad directa.

Para apoyar el llenado de la tabla es importante conocer la gráfica que relaciona las variables: grados Celsius y grados Fahrenheit.

 

PISTAS PARA EL LLENADO DE TU TABLA

En la gráfica, en el eje “x” se representan las cantidades de grados Celsius y en el eje “y” se encuentran las cantidades en grados Fahrenheit.

Como puedes observar, la gráfica sí es una recta, pero no pasa por el origen. Así que, ya puedes completar las dos celdas correspondientes de tu tabla con la palabra No. Con esto es suficiente para determinar que no se trata de una relación de proporcionalidad directa.

También se observa que si las cantidades correspondientes a los grados Celsius aumentan: diez, veinte, treinta, cuarenta, etc., también lo hacen las de los grados Fahrenheit: 20, 40, 60, 70, etc. Pero no lo hacen en la misma proporción. Por lo tanto, se escribe No en la celda correspondiente de la tabla.

Falta verificar una característica más: ¿Existe constante de proporcionalidad entre las variables?, ¿cómo puedes saberlo?

Se sabe que la constante de proporcionalidad se simboliza con la letra “k” y es el cociente que se obtiene de la división de la primera variable “y” entre la variable “x”. El número que se obtiene es constante, esto quiere decir que, aunque cambien las cantidades de las variables “x” y “y”, el cociente no cambia.

Verifica si existe o no constante de proporcionalidad, para ello, usa la fórmula. La variable “x” corresponde a los grados Celsius y la variable “y”, corresponde a los grados Fahrenheit.

 

ACTIVIDAD 3.

Eje: Número, Álgebra y Variación.

Tema: Funciones.

Aprendizaje Esperado: Analiza y compara situaciones de variación lineal y proporcionalidad inversa a partir de sus representaciones tabular, gráfica y algebraica. Interpreta y resuelve problemas que se modelan con este tipo de variación, incluyendo fenómenos de la física y otros contextos.

Énfasis: Analizar y comparar situaciones de variación lineal y proporcionalidad inversa.

Completa la siguiente tabla:

Grados Celsius	Grados Fahrenheit	Coordenadas
-25°	-13	( -25, -13)
-20°
-15°
-10°
-5°
5°	41	( 5, 41)
10°
15°
20°
25°

 

Por ejemplo, para saber cuántos grados Fahrenheit corresponden a 5 grados Celsius, se sustituye en la fórmula el número 5 en la variable grados Celsius y se realiza las operaciones correspondientes:

 

Fórmula: °F = 1.8°C + 32

Sustituyendo 5°C: °F = 1.8 (5) + 32

Realizando operaciones: °F = 9 + 32 = 41

Coordenadas: (5, 41)

Entonces: 5°C = 41°F

 

Por lo tanto, a 5 grados Celsius le corresponden 41 grados Fahrenheit. Así, se determina la primera coordenada: 5 corresponde a “x” y 41 corresponde a “y”. Ahora, calcula las otras coordenadas con: -20, -15, -10, -5, 10, 15, 20 y 25 grados Celsius.

Posteriormente realiza una gráfica con los datos obtenidos colocando las coordenadas que te resultaron.

Ahora, verifica si existe constante de proporcionalidad en la relación entre grados Celsius y Fahrenheit. Para hacerlo, se dividen los valores de la variable “y” entre los de la variable “x”, es decir, los grados Fahrenheit entre los grados Celsius con las tres coordenadas que se conocen.

Si en una variación lineal los valores de la variable “x” crecen, también crecen los de “y”. En una variación de proporcionalidad directa hay una condición: el aumento o disminución entre los valores siempre es en la misma proporción, además, la gráfica que la representa pasa por el origen del plano cartesiano.

Las expresiones algebraicas que caracterizan este tipo de variación tienen la forma:

 

Como en el problema de los grados Celsius y Fahrenheit, donde las variables “x” y “y”, se sustituyen por grados Celsius y grados Fahrenheit, pero también donde el parámetro “m” corresponde al número 1.8 y la “b” corresponde a 32.

ACTIVIDAD 4.

Eje: Número, Álgebra y Variación.

Tema: Funciones.

Aprendizaje Esperado: Analiza y compara situaciones de variación lineal y proporcionalidad inversa a partir de sus representaciones tabular, gráfica y algebraica. Interpreta y resuelve problemas que se modelan con este tipo de variación, incluyendo fenómenos de la física y otros contextos.

Énfasis: Analizar y comparar situaciones de variación lineal y proporcionalidad inversa.

 

Primer ejemplo:

Donde:

m = 2

b = 3

 

Segundo ejemplo:

Donde:

m = -2

b = 3

 

Tercer ejemplo:

Donde:

m = un medio

b = 3

 

¿Sabes por qué en todos los ejemplos, “b” es igual a 3? “b” puede ser cualquier número real, en este caso, los ejemplos presentan al parámetro (b = 3), esto para observar lo siguiente.

Es importante recuperar que al parámetro “m” se le conoce como pendiente de la recta y al parámetro “b” se le llama ordenada al origen.

Observa las tres ecuaciones representadas en estos ejes de coordenadas.

 

Todas tienen diferentes pendientes, pero la misma ordenada al origen. Las pendientes son: -2, 2 y un medio, respectivamente. Mientras la ordenada al origen en todas es tres. La pendiente de una recta se relaciona con el ángulo de inclinación de la recta. Como puedes observar, unas rectas están más inclinadas que otras. Y todas coinciden en el punto (0,3), que es donde cruzan al eje de las “y”, lo que se llama ordenada al origen, representado por el parámetro “b”.

Después de esta información, analiza los siguientes ejemplos relacionados con la inclinación de la recta, para aclarar a qué se refiere la pendiente de una recta. Observa las siguientes imágenes:

La imagen de la izquierda representa una señal de tránsito indicando que se aproxima una pendiente en la carretera. La de la derecha representa la pendiente que existe en un tramo de carretera.

¿Entonces, si una carretera está plana significa que no tiene pendiente? Efectivamente, también se puede decir que la pendiente de esa carretera es cero.

Si observas las siguientes gráficas de las rectas “A” y “B”, notarás que tienen diferentes pendientes.

La recta “A” está más inclinada que la recta “B”, es decir, tienen diferente ángulo de inclinación. Observa el ángulo de inclinación que forma cada una de las rectas con el eje de las abscisas o eje “x”.

Por ejemplo, la recta A forma un ángulo con el eje “x”, que se identifica con la letra “c”, este ángulo se llama ángulo de inclinación. ¿Cuál es el ángulo inclinación de la recta B?

Seguramente pensaste en el ángulo representado con la letra “d”, Observa que es mayor el ángulo “c” que el ángulo “d”, por lo tanto, la recta A tiene mayor pendiente que la recta B.

Retoma las gráficas de las tres rectas para concluir el análisis de la pendiente.

Las pendientes son (m = -2), (m = 2) y (m = 1/2). Analiza primero las dos pendientes positivas, es decir, con “m” igual a 2 y “m” igual a un medio.

Como 2 es mayor que un medio, la recta y = 2x + 3, tiene mayor pendiente que la recta y = 1/2x + 3. Pero ¿qué ocurre con la pendiente negativa de la gráfica de la ecuación y = -2x + 3?

Observa que la recta y = -2x + 3, es completamente simétrica a la recta y = 2x + 3, es decir, si se piensa en el eje “y” como espejo, la recta con pendiente negativa refleja a la recta con pendiente positiva. Esto sucede porque los valores de “m” en esas rectas también son simétricos.

Para que no haya duda respecto a la pendiente negativa, compara otro par de rectas, una con pendiente positiva y otra con pendiente negativa.

Estas rectas no son simétricas, la recta y = x + 4 tiene pendiente 1 y la recta y = -2x + 1 tiene pendiente negativa.

Observa que la recta con pendiente positiva se inclina hacia la derecha con respecto al eje “y” y la recta con pendiente negativa se inclina hacia la izquierda. También puedes notar que el ángulo “c” de la recta con pendiente positiva, es agudo, es decir, menor a 90 grados, en cambio el ángulo “d”, de la recta con pendiente negativa es un ángulo obtuso, es decir, un ángulo mayor a 90 grados pero menor a 180 grados.

Ahora, reflexiona en lo siguiente: ¿qué sucede si la recta tiene un ángulo de inclinación de cero grados? La recta sería paralela al eje “x”, como la recta A de la siguiente imagen. Tiene una pendiente de valor cero.

Si la recta es completamente vertical, es decir, si es paralela al eje “y”, como la recta B, ¿cuál es su pendiente? En este caso la recta no está definida, significa que la pendiente no existe para una recta así.

En la forma general de la variación lineal (y = m x + b), a la “b” se le conoce como ordenada al origen.

En los siguientes ejemplos, las ordenadas al origen (b) son: 4, 8 y -6, respectivamente.

 

Ejemplo 1: y = 5x + 4

Ejemplo 2: y = -3x + 8

Ejemplo 3: 7x - 6

Ahora, retoma las gráficas de las tres y observa que en todas, la ordenada al origen, es decir, la letra “b” es igual a 3.

Puedes identificar que las tres rectas pasan por el mismo punto al cortar al eje de las “y”. Seguramente ya sabes que es tres. Reflexiona: ¿cuáles son las coordenadas de ese punto?

Las coordenadas son: (0, 3). Las tres rectas comparten esta coordenada, y significa que cuando la variable “x” es cero, la variable “y” será tres.

 

Entonces:

¿Por qué punto del eje de las “y”, pasará la recta: y = 9x - 5?

¿Cuál son las coordenadas de ese punto?

La recta (y = 9x – 5), cruza al eje “y” en el punto -5. Las coordenadas de ese punto son (0, -5).

Ahora, reflexiona en la siguiente cuestión:

¿Qué sucede con la recta cuando el parámetro “b” vale cero?

Es lo mismo que la ecuación:

Si “b” es igual a cero, indica una variación proporcional. Se sabe que la constante “k” en una variación proporcional, se calcula dividiendo los valores de la variable “y” entre los valores correspondientes de la variable “x”. En forma general:

En la forma general de la constante “k”. Despeja la variable “y”.

Por lo tanto, se puede ver que el ejemplo (y = 6x) tiene la misma forma que la ecuación general, esto significa que es una variación proporcional donde la constante “k” es 6.

Se ha comparado la variación lineal de la forma (y = m x + b) con la variación proporcional directa, pero ¿qué sucede con la variación proporcional inversa?, ¿tienen alguna característica en común? Estas variables no comparten ninguna característica en común, pero si se pueden decir las características principales de la variación proporcional inversa. 

 

ACTIVIDAD 5.

Eje: Número, Álgebra y Variación.

Tema: Funciones.

Aprendizaje Esperado: Analiza y compara situaciones de variación lineal y proporcionalidad inversa a partir de sus representaciones tabular, gráfica y algebraica. Interpreta y resuelve problemas que se modelan con este tipo de variación, incluyendo fenómenos de la física y otros contextos.

Énfasis: Analizar y comparar situaciones de variación lineal y proporcionalidad inversa.

 

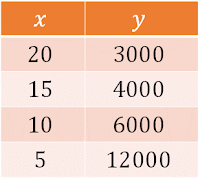
Situación-problema: cajas de naranjas

Para empacar una cosecha de naranjas se requieren 3,000 cajas, colocando 20 kilogramos de naranjas en cada caja. ¿Cuántas cajas se necesitan si ahora se quieren colocar solamente 15 kilos, 10 kilos y 5 kilos en cada caja? 

En una variación inversa, cuando una de las magnitudes crece, la otra disminuye; por ello, entre más kilos de naranja se coloquen en una caja, disminuirá la cantidad de cajas que se necesiten.

“x” será el número de kilogramos y “y” la cantidad de cajas que se necesitan.

 

Observa en la siguiente tabla que, mientras las cantidades de “x” disminuyen las cantidades de “y” aumentan. Así, para cajas con 20 kilos se requieren 3,000 cajas, para cajas con 15 kilos se requieren 4,000 cajas, y así sucesivamente.

En una variación proporcional inversa: Si la variable “x” aumenta, entonces disminuye la variable “y”, y si la variable “x” disminuye, aumenta la variable “y” de manera proporcional. Por ejemplo, si la cantidad de cajas disminuye a la mitad, la cantidad de naranjas aumenta al doble.

En la tabla anterior, se puede observar que si la cantidad de kilos por caja (15 por ejemplo) disminuye a la tercera parte, es decir a 5 kilos, la cantidad de cajas (4,000 para 15 kilos) aumenta al triple (12,000 para 5 kilos por caja).

En la variación proporcional inversa también existe una constante de proporcionalidad. Observa lo que sucede si se multiplican las cantidades de la variable “x” por las cantidades correspondientes de la variable “y”.

El resultado es 60 mil, un número constante. En toda variación proporcional inversa al multiplicar las cantidades correspondientes de “x” y “y” el resultado representa a la constante de proporcionalidad simbolizada con la letra “k”, por lo tanto, “k” es igual a “x” por “y”.

 

En la variación lineal, sea o no proporcional, la gráfica es una línea recta. Como puedes observar, la gráfica de la variación proporcional inversa es una curva llamada hipérbola.

 

Observa cómo la curva se acerca a los ejes, pero no los llega a tocar, esto es independiente de los valores que le asignen a la variable “x”. Puedes comprobarlo asignando los valores que desees a la variable “x” para obtener los de “y”.

Al despejar “y” de la ecuación, se obtiene “y” igual a “k” entre “x”. En el problema, “k” es igual 60 mil, por lo tanto, “y” es igual 60 mil entre “x”.

Usando esta fórmula puedes obtener los valores de “y” y comprobar que la curva nunca toca los ejes “x” y “y”. Utilicen esta misma fórmula y calcula el número de cajas que se necesitarán si cada caja contuviera 25, 30 y 35 kilos de naranjas. 

Completa la siguiente tabla para distinguir las características más importantes de cada una de estas variaciones. Escribe un tache donde corresponda.

ACTIVIDAD EXTRA.

Eje: Número, Álgebra y Variación.

Tema: Funciones.

Aprendizaje Esperado: Analiza y compara situaciones de variación lineal y proporcionalidad inversa a partir de sus representaciones tabular, gráfica y algebraica. Interpreta y resuelve problemas que se modelan con este tipo de variación, incluyendo fenómenos de la física y otros contextos.

Énfasis: Analizar y comparar situaciones de variación lineal y proporcionalidad inversa.

 

Retoma la situación de los grados Fahrenheit y grados Celsius. Las coordenadas por la que pasa la recta son (0, 32), porque el parámetro “b” en esta ecuación es igual a 32.

1._ ¿Qué significa esto en el problema planteado inicialmente?

Significa que cuando en algún un lugar la temperatura está a cero grados Celsius, la temperatura en ese lugar es de 32 grados Fahrenheit. Esto se puede comprobar si se sustituye en la fórmula cero grados Celsius, lo multiplicas por 1.8 y sumas 32, el resultado será 32.

Entonces, cuando la temperatura en el puerto de Veracruz está a 80 grados Fahrenheit: ¿cuántos grados Celsius son?, ¿es posible utilizar la misma fórmula?

Sí es posible utilizar esta fórmula, sólo habrá que despejar los grados Celsius. Presta atención al procedimiento:

Primero, aplica la propiedad uniforme, restando 32 en cada lado de la igualdad. Haciendo operaciones, grados Fahrenheit menos treinta y dos es igual a uno punto ocho grados Celsius más cero, ya que treinta y dos menos treinta y dos es igual a cero.

 

Aplicando el neutro aditivo, grados Fahrenheit menos treinta y dos es igual a uno punto ocho grados Celsius.

Después, se divide uno punto ocho de cada lado de la igualdad. Haciendo operaciones, grados Fahrenheit menos treinta y dos, todo esto entre uno punto ocho es igual a grados Celsius.

 

Finalmente, se aplica la propiedad simétrica de la igualdad que permite intercambiar los lados de la igualdad sin alterarla.

Todavía falta sustituir los 80 grados Fahrenheit en la fórmula y hacer las operaciones para saber cuánto calor hacía ese día en Veracruz.

 

La temperatura fue de casi 27 grados Celsius, es decir, hacía calor en Veracruz, pero no demasiado.

Durante la sesión se ha estudiado el tema de la variación lineal, comparándola con la variación proporcional directa y la variación proporcional inversa.

Es importante que elabores tus notas, considerando las ideas más importantes de la sesión, resuelve las actividades planteadas y, sobre todo, anota tus dudas y posibles dificultades.