1°A Matemáticas, 31 de Mayo - 4 de Junio

 

Materia: M a t e m á t i c a s    I

Nombre del docente: Lizbeth Hamid Carpinteyro Montiel

Correo electrónico: halimoca@hotmail.com

Fecha: Del lunes 31 de mayo al viernes 4 de junio del año 2021.

¡Hola jóvenes!

Si tienen dudas comuníquense conmigo mediante el correo electrónico o enviando un mensaje por whatsApp. En caso de que sea por correo electrónico en ASUNTO coloquen DUDAS y serán resueltas a la mayor brevedad posible. 

Recuerden que al enviar sus actividades por correo electrónico deben escribir en ASUNTO: Nombre completo, Grado y Grupo.

 

INDICACIONES GENERALES:

• Copia el tema completo e indicaciones en tu libreta de matemáticas.
• Envía las fotografías al correo electrónico, debes revisar que las fotografías sean claras y se pueda leer perfectamente tu trabajo, de lo contrario se te regresará sin evaluar.
• Colocar nombre completo, grado y grupo a CADA HOJA.

CLASE A DISTANCIA:

Entrar a la clase en línea; día LUNES.

1._ Entrar con el nombre completo del alumno.

2._ El enlace de la clase se enviara 5 minutos antes de la clase en el grupo de whatsApp de Matemáticas.

La clase será de 1:40 a 2:20 pm los días LUNES.

 

ACTIVIDAD 1.

Eje: Forma, Espacio y Medida.

Tema: Magnitudes y Medidas.

Subtema: Perímetro y área.

Aprendizaje Esperado: Calcula el perímetro de polígonos y del círculo, y áreas de triángulos y cuadriláteros desarrollando y aplicando fórmulas.

Énfasis: Usar expresiones algebraicas equivalentes para representar el perímetro y área de figuras geométricas.

 

La construcción es fundamental en el desarrollo social y conocer sobre las distintas formas geométricas y sus medidas, así como el perímetro y el área, es muy importante.

La forma de medir ha cambiado a lo largo del tiempo, pero la necesidad de hacer mediciones sigue existiendo; dado que, en toda actividad humana, se requieren mediciones de algún tipo. Observa el siguiente vídeo y elabora un mapa conceptual o cuadro sinóptico.

Obtención del perímetro en la antigüedad 

En la actualidad, existen técnicas de medición modernas, con instrumentos muy precisos.

¿Qué instrumentos conoces que se usen para medir? R=

Tal vez el instrumento para la medición del perímetro más común, en este contexto, sea el flexómetro (metro).

 

 

ACTIVIDAD 2.

Eje: Forma, Espacio y Medida.

Tema: Magnitudes y Medidas.

Subtema: Perímetro y área.

Aprendizaje Esperado: Calcula el perímetro de polígonos y del círculo, y áreas de triángulos y cuadriláteros desarrollando y aplicando fórmulas.

Énfasis: Usar expresiones algebraicas equivalentes para representar el perímetro y área de figuras geométricas.

Contesta las siguientes preguntas:

1._ ¿Qué media el hombre con la longitud de sus pasos? R=

2._ ¿Qué utilizaba para medir extensiones de tierra menores? R=

3._ ¿Qué empleaba para mediciones verticales? R=

4._ ¿Cómo se medía el codo? R=

5._ ¿Qué utilizaban para las mediciones horizontales más pequeñas? R=

6._ ¿Cómo se medía la cuarta? R=

7._ Actualmente, ¿Cuánto mide el codo? R=

8._ ¿Qué utilizaban los chinos para medir longitudes? R=

9._ Actualmente, ¿cuánto mide el “Chi”? R=

10._ ¿Qué se utilizaba para medir longitudes más grande en la antigua Grecia y en Egipto? R=  

11._ ¿Qué utilizaron los romanos? R=

12._ ¿A cuánto equivalía la milla romana? R=

13._ ¿Qué utilizaban los chinos? R=

14._ Actualmente, ¿a cuánto equivale el “Li”? R=

15._ ¿Dónde vivían los babilonios? R=

16._ ¿Cómo llamó Heródoto a los agrimensores? R=

17._ ¿Qué herramientas utilizaban? R=

18._ ¿Dónde se encuentra uno de los primeros ejemplos de una medición de terreno, utilizando medios matemáticos? R=

19._ ¿Aproximadamente cuándo se construyó “La gran pirámide”? R=

20._ ¿Dónde se ubica “La gran Pirámide”? R=

 

 

ACTIVIDAD 3.

Eje: Forma, Espacio y Medida.

Tema: Magnitudes y Medidas.

Subtema: Perímetro y área.

Aprendizaje Esperado: Calcula el perímetro de polígonos y del círculo, y áreas de triángulos y cuadriláteros desarrollando y aplicando fórmulas.

Énfasis: Usar expresiones algebraicas equivalentes para representar el perímetro y área de figuras geométricas.

Para verificar la diversidad de medidas entre pie, cuarta y codo; mide con una regla:

• Longitud de un paso largo tuyo, haz una marca en el piso y da un paso largo y mide desde la marca hasta donde llegaste.
• Tu pie, Desde el inicio del dedo gordo hasta donde termina el talón de tu pie.
• Tu cuarta, mide desde el dedo meñique (el más chiquito) hasta el dedo pulgar (el gordito) con los dedos separados.
• Tu codo, mide desde donde inicia tu codo hasta la punta del dedo medio.

 

ACTIVIDAD 4.

Eje: Forma, Espacio y Medida.

Tema: Magnitudes y Medidas.

Subtema: Perímetro y área.

Aprendizaje Esperado: Calcula el perímetro de polígonos y del círculo, y áreas de triángulos y cuadriláteros desarrollando y aplicando fórmulas.

Énfasis: Usar expresiones algebraicas equivalentes para representar el perímetro y área de figuras geométricas.

 

Calcula el perímetro de la figura.

En una secundaria, se va a reforestar un espacio que tiene  forma de hexágono irregular, como la que se muestra en la imagen. En todo el contorno, se va a colocar una cerca de metal.

¿Cuál es el perímetro de la figura si, con el flexómetro (metro), se obtuvieron las medidas descritas? R= 

El perímetro se calcula sumando la longitud de todos los lados de una figura.

De manera general, se puede expresar que: el perímetro de cualquier figura es la medida de la longitud alrededor de ella.

ACTIVIDAD 5.

Eje: Forma, Espacio y Medida.

Tema: Magnitudes y Medidas.

Subtema: Perímetro y área.

Aprendizaje Esperado: Calcula el perímetro de polígonos y del círculo, y áreas de triángulos y cuadriláteros desarrollando y aplicando fórmulas.

Énfasis: Usar expresiones algebraicas equivalentes para representar el perímetro y área de figuras geométricas.

 

Lee y copia la siguiente información:

En un polígono, el perímetro es la medida de la longitud total que suman todos sus lados.

En un círculo, el perímetro es el la longitud de la circunferencia que lo rodea; entonces el perímetro delimita a una figura.

La fórmula para calcular el perímetro de un cuadrado es p=l+l+l+l; donde “p” representa el valor del perímetro y “l” representa la longitud de cada uno de sus lados, que también es equivalente a la expresión p=4l, o bien p=4 por “l”, pues se conoce que un cuadrado tiene la misma longitud en cada uno de sus lados.

Estas fórmulas son expresiones algebraicas. Una expresión algebraica es una combinación de literales (letras que sirven para representar cantidades) y números que, en algunos casos, representan coeficientes (números junto a las letras) que las multiplican.

Por ejemplo, en la expresión algebraica para encontrar el perímetro del cuadrado p = 4ele, el coeficiente cuatro multiplica a la literal ele.

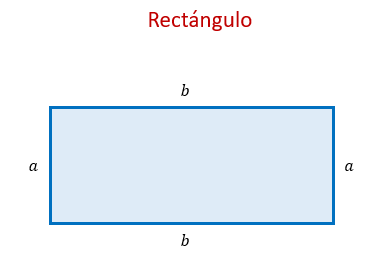
Un rectángulo es un cuadrilátero, cuyos lados forman ángulos rectos. A diferencia del cuadrado, no todos los lados son iguales entre sí. Existe igualdad de longitud sólo en los lados que son opuestos entre sí.

Es posible representar esta característica asignando una literal a cada lado, tal como aparece en la figura.

En este caso, se usa la literal “b” para representar la longitud de la base y se usa la literal “a” para representar la longitud de la altura.

Sin embargo, pueden utilizarse otras literales como “x” o “y”.

Entonces, utilizando la fórmula del  perímetro del rectángulo, analiza las siguientes expresiones algebraicas equivalentes:

A partir de la expresión p = a + a + b + b, es posible agrupar términos semejantes y obtener la expresión: p = (a + a) + (b + b), que es equivalente a la expresión p = 2a + 2b.

Por otro lado, usando un orden diferente de la misma expresión, puede representarse como:           p= a + b + a + b; aquí, es posible agrupar p= (a + b) + (a + b), que es equivalente a              p=2 (a + b). Al aplicar la propiedad distributiva de la multiplicación, obtienes la expresión inicial: p = 2a + 2b.

Por ejemplo, si la base del rectángulo mide 5 cm y la altura mide 8 cm; entonces, sustituyendo estos valores en la expresión p=2(a + b), donde “p” es el perímetro, “b” es la base y “a” la altura, encuentran que “p” es igual a dos veces la suma de la base más la altura; es decir, p = 2 por la suma 8 + 5, que es igual a 2 por 13, igual a 26 cm. Las unidades son lineales porque se trata de una longitud, la longitud del contorno del rectángulo.