2°A Matemáticas, 31 de Mayo - 4 de Junio

 

Materia: M a t e m á t i c a s    I I

Nombre del docente: Lizbeth Hamid Carpinteyro Montiel

Correo electrónico: halimoca@hotmail.com

Fecha: Del lunes 31 de mayo al viernes 4 de junio del año 2021.

¡Hola jóvenes!

Si tienen dudas comuníquense conmigo mediante el correo electrónico o enviando un mensaje por whatsApp. En caso de que sea por correo electrónico en ASUNTO coloquen DUDAS y serán resueltas a la mayor brevedad posible. 

Recuerden que al enviar sus actividades por correo electrónico deben escribir en ASUNTO: Nombre completo, Grado y Grupo.

 

INDICACIONES GENERALES:

• Copia el tema completo e indicaciones en tu libreta de matemáticas.
• Envía las fotografías al correo electrónico, debes revisar que las fotografías sean claras y se pueda leer perfectamente tu trabajo, de lo contrario se te regresará sin evaluar.
• Colocar nombre completo, grado y grupo a CADA HOJA.

CLASE A DISTANCIA:

Entrar a la clase en línea; día LUNES.

1._ Entrar con el nombre completo del alumno.

2._ El enlace de la clase se enviara 5 minutos antes de la clase en el grupo de whatsApp de Matemáticas.

La clase será de 2:25 a 3:05 pm los días LUNES.

 

ACTIVIDAD 1.

Eje: Forma, Espacio y Medida.

Tema: Magnitudes y Medidas.

Subtema: Volumen de prismas rectos.

Aprendizaje Esperado: Calcular el volumen de prismas y cilindros rectos.

Énfasis: Dar sentido y significado al cálculo del volumen de prismas rectos.

Lee y contesta las preguntas.

“La geometría es el arte de pensar bien y dibujar mal” fue lo que alguna vez dijo Henri Poincaré, y es que lograr la perfección en los trazos de las figuras cuyas propiedades son complejas, no es tarea fácil. Está semana estudiaras los prismas rectos.

1._ ¿Alguna vez has tenido que comprar una caja para guardar un regalo?

2._ ¿O has tenido que construir alguna?

En algunas asignaturas de la universidad, para las áreas de diseño gráfico, piden que los alumnos elaboren cajas, con diseños prácticos y económicos que puedan ser de utilidad para alguna empresa, por ejemplo, en algunas cadenas de alimentos.

Independientemente del material con el que se elabore la caja, es conveniente que, en primer lugar, se elabore su desarrollo plano, como el que se muestra en la siguiente imagen.

Recortando el desarrollo y doblándolo por los lados de cada uno de los polígonos que lo forman, podemos armar una caja.

Si recortas la figura tal cual, te costará un poco de trabajo armar la caja porque no tiene pestañas.

Las pestañas son aquellas secciones del desarrollo plano que permiten mantener fijas las caras contiguas cuando armamos el prisma.

3._ ¿Qué forma tendrá la caja que se puede armar con este desarrollo plano?

En el siguiente esquema puedes observar las pestañas y con ellas puedes mantener fijas las caras del prisma. Al hacer esto, puedes armar la caja que tiene forma de cubo.

4._ ¿Será el único desarrollo plano con el cual podemos armar una caja de esa forma?

5._ ¿O cualquier desarrollo plano con 6 caras cuadradas podrá formar una caja cúbica?

Te presentaremos otro diseño formado con 6 cuadrados para analizar si todos corresponden al desarrollo plano de un cubo, es decir, si con esos diseños es posible construir un cubo.

6._ ¿Piensas que con ese desarrollo plano se pueda formar una caja cúbica? R=

7._ ¿Por qué? R=

8._ ¿Qué características deberá tener un desarrollo plano para que pueda armarse una caja? R=

Observa los desarrollos y encierra con verde los que se pueden armar para formar una caja y con rojo los que no se pueden armar.

Supón que eres una o un diseñador gráfico y diseñaras una caja para guardar regalos, entre tus diseños se encuentran los siguientes.  Observa atentamente los desarrollos planos que se muestran.

1._ ¿Cuál o cuáles de estos piensas que permiten construir una caja en forma de cubo? R=

En este momento no tomes en cuenta las pestañas del desarrollo plano.

Puedes trazar los desarrollos en alguna hoja de tu cuaderno o papel de reúso, recortarlos e intentar armar una caja. El que se encuentra señalado con el número 1 fue el que se presentó en la actividad 1, aunque ahora se encuentra en otra posición. En aquel momento se afirmó que este desarrollo plano sí corresponde a un cubo.

ACTIVIDAD 2.

Eje: Forma, Espacio y Medida.

Tema: Magnitudes y Medidas.

Subtema: Volumen de prismas rectos.

Aprendizaje Esperado: Calcular el volumen de prismas y cilindros rectos.

Énfasis: Dar sentido y significado al cálculo del volumen de prismas rectos.

Analiza la siguiente situación y contesta las preguntas:

Se producirán unos chocolates en forma de prisma triangular, y para ello, han pedido al diseñador que realice algunos prototipos de caja para contener el chocolate.

1._ ¿De qué forman diseñarías una caja con forma de prisma triangular? R=

2._ ¿La harías como la que se muestra en la siguiente imagen? R=

3._ ¿Puede considerarse que la caja armada es un prisma? R=

4._ ¿Qué es necesario tomar en cuenta para construirla? R=

5._ ¿Consideras que el desarrollo plano que se muestra a continuación podrá formar un prisma triangular? R=

 

6._ Imagina cómo se doblaría el desarrollo plano para poder armarse. ¿Qué características deben tener la posición de las caras que serán sus bases? R=

7._ ¿Consideras que esta segunda figura también forma una caja? R=

8._ ¿Qué características tiene el segundo desarrollo plano que le permite o no armar la caja en forma de prisma triangular? R=

9._ ¿Qué pasaría si en lugar de caras laterales en forma de rectángulo, se incluyen caras laterales en forma de cuadrado? R=

10._ ¿La caja armada dejaría de ser un prisma? R=

11._ ¿Podría armarse un prisma con ella? R=

 

Como seguramente ya lo notaste, por todos lados existen prismas, sobre todo en actividades de venta de productos, por ejemplo, en los empaques de medicina y de alimentos. Esto significa que, muchas veces, los diseñadores tienen que realizar un desarrollo plano que pueda fabricarse en serie.

ACTIVIDAD 3.

Eje: Forma, Espacio y Medida.

Tema: Magnitudes y Medidas.

Subtema: Volumen de prismas rectos.

Aprendizaje Esperado: Calcular el volumen de prismas y cilindros rectos.

Énfasis: Dar sentido y significado al cálculo del volumen de prismas rectos.

Analiza la siguiente situación y contesta las preguntas:

Una empresa de tostadas empacará cierta cantidad de su producto por empaque y, además, elaborará otra presentación más económica donde solo empacará la mitad de las tostadas del primer empaque, sin modificar el tamaño de su producto.

La empresa desea que los empaques sean como el que se muestra en la siguiente imagen.

Si el empaque que se muestra es la primera presentación.

1._ ¿Qué medida o medidas piensas que se le debe modificar para el empaque contenga la mitad del producto sin modificar la medida de las tostadas? R=

2._ ¿Qué desarrollo plano permitiría la construcción de la primera caja y qué desarrollo plano permitiría la construcción de la caja para la mitad de tostadas? R=

3._ Imagina distintos desarrollos para la primera caja y dibújalos en tu cuaderno.

4._ ¿Qué forma tendrán las caras laterales y cuántas caras laterales tendría? R=

5._ ¿Consideras que el siguiente desarrollo plano permitirá construir la primera caja? R=

6._ Tomando como referencia ese desarrollo plano, ¿Qué cambiarías para que pueda contener la mitad de las tostadas? R=

7._ ¿Reducirían el tamaño de la base a la mitad, como en el desarrollo plano que se muestra? R=

8._ ¿Qué desarrollo plano construirías para cumplir con las condiciones mencionadas? R=

Ahora, se muestra otro desarrollo plano.

9._ ¿Consideras que con él sí podremos empaquetar la mitad de las tostadas? R=

10._ ¿Qué características tiene el nuevo desarrollo plano que lo hacen diferente al anterior? R=

11._ Observa este nuevo desarrollo plano, ¿consideras que permitirá construir la caja con menor cantidad de tostadas? R=

12._ ¿Qué hace diferente a este desarrollo plano del anterior? R=  

 

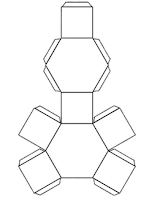
Observa como existe más de una manera para construir el desarrollo plano, que al armarse formen prismas iguales, en este caso, un prisma hexagonal.

 

En la imagen se observan los tres desarrollos planos mostrados para un prisma hexagonal.

13._ En tu cuaderno escribe, las características que deben tener para que pueda formarse un prisma, independientemente de la forma de la base. 

ACTIVIDAD 4.

Eje: Forma, Espacio y Medida.

Tema: Magnitudes y Medidas.

Subtema: Volumen de prismas rectos.

Aprendizaje Esperado: Calcular el volumen de prismas y cilindros rectos.

Énfasis: Dar sentido y significado al cálculo del volumen de prismas rectos.

Elabora los desarrollos planos que te solicitan y contesta las preguntas.

Analiza otro caso cotidiano en donde la construcción y armado de prismas juegan un papel importante.

Algunas empresas producen y empaquetan pañuelos desechables, como los que se muestran en la siguiente imagen.

Aunque la cara superior tiene una ranura por donde se pueden tomar los pañuelos desechables, la caja es un prisma rectangular. Cumple con las características de los prismas, entre ellas, tener dos bases iguales y paralelas, rectángulos en este caso, y caras laterales rectangulares.

1._ Elaborar el desarrollo plano de la caja, dibújalo en tu cuaderno.

2._ ¿Qué características tiene el desarrollo plano que imaginaste y dibujaste? R=

3._ El siguiente desarrollo plano. ¿Nos permite construir una caja parecida a la mostrada anteriormente? R=
 

 

Con este desarrollo plano es posible construir un prisma como el de la caja de pañuelos desechables.

4._ ¿Será éste el único desarrollo plano que permite construir una caja como la de los pañuelos desechables?

5._ Dibuja otro desarrollo plano que genera la misma caja de pañuelos desechables.

 

ACTIVIDAD 5.

Eje: Forma, Espacio y Medida.

Tema: Magnitudes y Medidas.

Subtema: Volumen de prismas rectos.

Aprendizaje Esperado: Calcular el volumen de prismas y cilindros rectos.

Énfasis: Dar sentido y significado al cálculo del volumen de prismas rectos.

Analiza, lee y copia las características de los prismas estudiados.

Retoma todos los prismas que se arman con los desarrollos planos que hemos visto en esta sesión y observa sus similitudes y diferencias.

Los prismas que se han estudiado son:

El prisma cuadrangular, cuyas caras laterales son iguales a sus bases, es decir, el cubo.

El segundo es el prisma triangular. Si consideremos que este prisma tiene dos caras triangulares y 3 rectangulares. Las dos caras triangulares serán sus bases y las que definirán el nombre del prisma.

El nombre del cuerpo geométrico de la caja de tostadas es prisma hexagonal.

El prisma formado en la caja de pañuelos desechables, es un prisma rectangular, porque al observarlo detenidamente, nos damos cuenta que todas sus caras son rectangulares.

Ahora que ya conoces el nombre de los prismas y la manera para nombrarlos, coloquemos cada uno de ellos sobre la base que le da nombre al prisma.

El lado que se destaca en color amarillo es el ancho de la base; La parte sombreada de color rosa es el área de la base y la altura del prisma es la medida del lado que se destaca en color verde.

Es importante que identifiques todos estos elementos en cada uno de los prismas, independientemente de la posición en la que se encuentren o independientemente del número de lados de la base de los prismas.

 

ACTIVIDAD  EXTRA.

Eje: Forma, Espacio y Medida.

Tema: Magnitudes y Medidas.

Subtema: Volumen de prismas rectos.

Aprendizaje Esperado: Calcular el volumen de prismas y cilindros rectos.

Énfasis: Dar sentido y significado al cálculo del volumen de prismas rectos.

Calcula el volumen del prisma hexagonal.

Recuerda los vídeos analizados en clase y encuentra el volumen del siguiente prisma hexagonal:

• Se sabe que la base de este prisma es un polígono regular, en este caso se trata de un hexágono.
• La medida de uno de sus lados es 10 cm.
• Su apotema mide 10.39 cm.
• La altura mide 15 cm.

 

Utiliza la siguiente fórmula:

V= Volumen

Ab= Área de la base

h= altura

P= Perímetro

a= apotema

2= Dividir entre 2 el resultado